labelssraka.blogg.se - Graph to equation maker

Used to name an algebraic expression in the variable x, can also be used to denote Pair that is paired with a specified first component. Compute answers using Wolframs breakthrough technology & knowledgebase, relied on by millions of students & professionals.

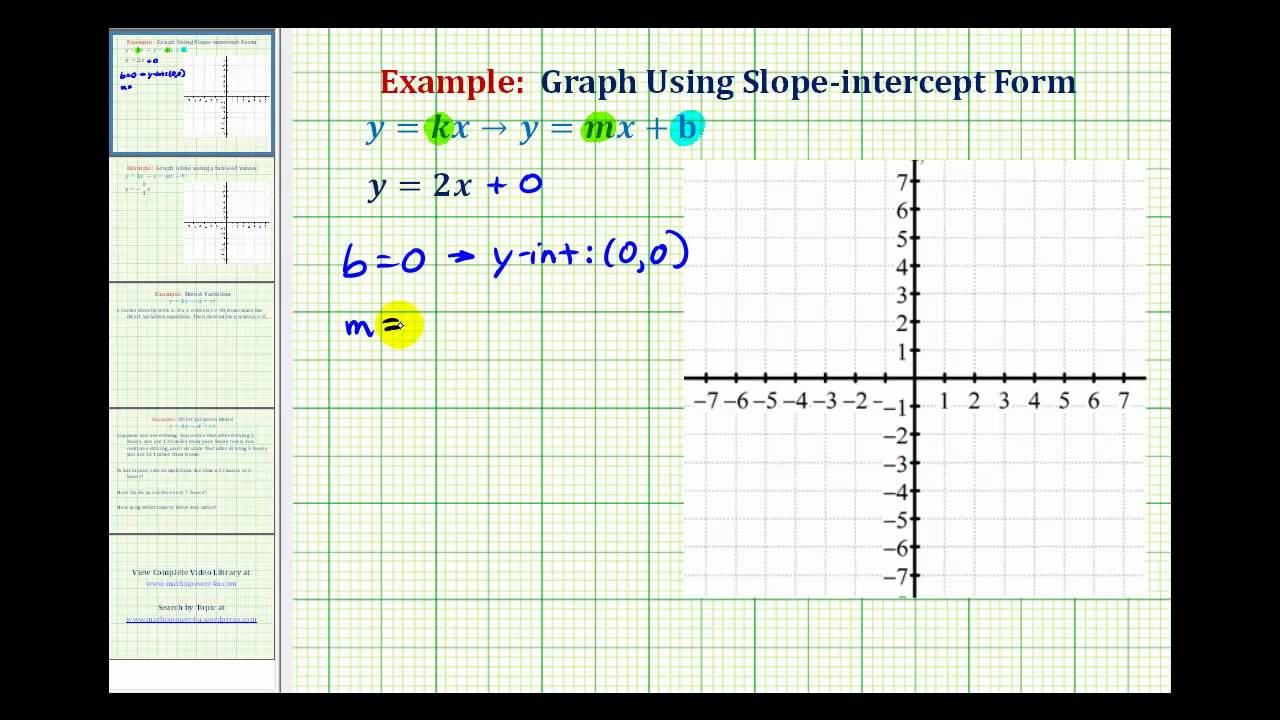
Sometimes, we use a special notation to name the second component of an ordered In this form, we obtain values of y for given values of x as follows: Now, dividing each member by 2, we obtain Solve 2y - 3x = 4 explicitly for y in terms of x and obtain solutions for x = 0,

Equal quantities are multiplied or divided by the same nonzero quantity.

The same quantity is added to or subtracted from equal quantities. Bing users found us today by using these math terms : Adding square root fractions, sheet for gmat, probability worksheets +.

Where we solved first-degree equations in one variable. In general, we can write equivalentĮquations in two variables by using the properties we introduced in Chapter 3, Of Equation (1), in that way getting y by itself. We obtained Equation (2) by adding the same quantity, -2x, to each member

We get the same pairings that we obtained using Equation (1) It is often easier to obtain solutions if equations are first expressed in such formīecause the dependent variable is expressed explicitly in terms of the independent In Equation (2), where y is by itself, we say that y is expressed explicitly in terms

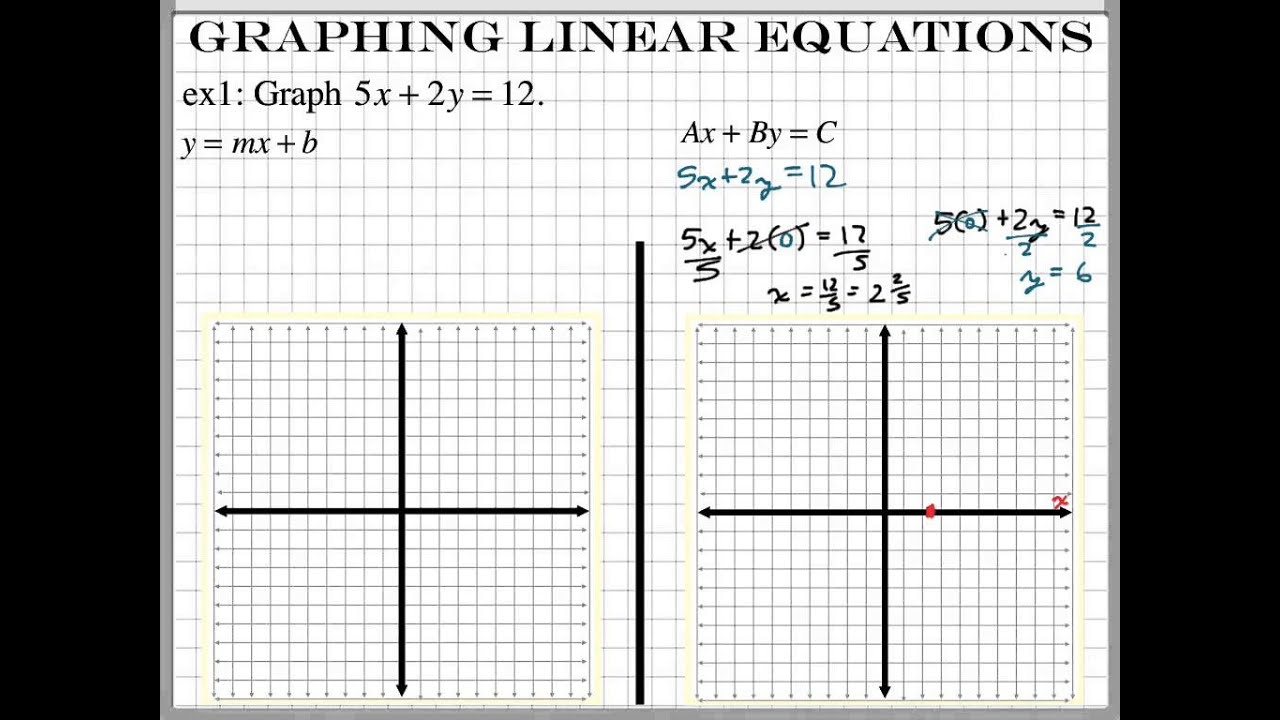
We can add -2x to both members of 2x + y = 4 to get The three pairings can now be displayed as the three ordered pairs Replacements for y are second components and hence y is the dependent variable.įor example, we can obtain pairings for equationīy substituting a particular value of one variable into Equation (1) and solving forįind the missing component so that the ordered pair is a solution to Ments for x are first components and hence x is the independent variable and If the variables x and y are used in an equation, it is understood that replace. It is convenient to speak of the variable associated with theįirst component of an ordered pair as the independent variable and the variableĪssociated with the second component of an ordered pair as the dependent variable. Of the variables, the value for the other variable is determined and thereforeĭependent on the first. In any particular equation involving two variables, when we assign a value to one Such pairings are sometimes shown in one of the following tabular forms. Some ordered pairs for t equal to 0, 1, 2, 3, 4, and 5 are With this agreement, solutions of theĮquation d - 40t are ordered pairs (t, d) whose components satisfy the equation. Second numbers in the pairs as components. We call such pairs of numbers ordered pairs, and we refer to the first and Order in which the first number refers to time and the second number refers toĭistance, we can abbreviate the above solutions as (1, 40), (2, 80), (3, 120), and If we agree to refer to the paired numbers in a specified The pair of numbers 1 and 40, considered together, is called a solution of theĮquation d = 40r because when we substitute 1 for t and 40 for d in the equation, The equation d = 40f pairs a distance d for each time t. In this chapter, we will deal with tabular and graphical representations. We have already used word sentences and equations to describe such relationships

4.Ě graph showing the relationship between time and distance.

Then, write the components of the equation as shown in the picture. First, select the cells you want to input the data in the future. You can follow the steps to graph an equation in excel without data. The distance traveled in miles is equal to forty times the number of hours traveled. Let’s say, we want to graph the equation of ymx+c. In a certain length of time by a car moving at a constant speed of 40 miles per hour. As an example, let us consider the distance traveled Plot families of graphs and describe their characteristics. Use graphs to solve optimisation problems. Find the equations of the translations and reflections of graphs of given functions. Slope of a line =§#xA0 m = y 2 - y 1 x 2 - x 1, \text to represent this ratio, where Δ is the Greek letter delta, which is used to mean "change in" a quantity.The language of mathematics is particularly effective in representing relationshipsīetween two or more variables. Identify and interpret roots, intercepts and turning points of quadratic functions graphically. One of the most helpful ways to determine the slope is to use the slope formula. In this resource, you investigated different ways to determine the slope of a linear function.